Cantilever Beam Demonstration

Alexander M. Tomsick - P.E. Director of Engineering

This video is part of a series of videos being produced to talk about the Voyager FDS sensor.

This video shows a comparison of dynamic strain and acceleration data collected on a cantilever beam. An example of a cantilever beam under bending is shown in Figure 1.

Figure 1: Cantilever Beam Under Bending

As the tip of the beam is deflected by the downward force (F), the beam experiences tensile strain on the top half of the beam and compressive strain on the bottom half of the beam. If this strain were measured, the tensile strain would lead to a positive measured value while the compressive strain would lead to a negative measured value. While the entire length of the beam will experience some amount of strain, the magnitude of this strain will be highest at the fixed end and decrease to zero towards the free end of the beam.

If the free end of the beam was initially held in the downward position shown in the Figure and was then released from the initial position, the beam would experience free vibration and vibrate primarily at its first natural frequency. Vibration of the beam at the first natural frequency will cause the free end of the beam to deflect upwards and downwards. The changing direction at the free end of the beam leads to oscillating strain fluctuating between tension and compression near the fixed support.

While the magnitude of strain is highest at the fixed end of the beam, the lack of displacement at the fixed end will lead to zero acceleration at this end of the beam. Since the maximum displacement occurs at the free end of the beam, the free end is where the maximum acceleration occurs.

What is a Microstrain

Before discussing the data collected from the cantilever beam using the Voyager FDS sensor, it is important to understand the relationship between the deformation of the sensor base plate and the measured strain amplitude. Typical strain amplitudes are very small, compared to the values calculated in the first two videos of this series. In practice, the strain measured on a hydrodynamic bearing will be very low, near five millionths of a strain (0.000005ε). Since these very small numbers can become difficult to work with, strain values are scaled by a factor of 1 million. This scaled value is denoted by (µε), which denotes the scaled unit of microstrain.

Example 1:

If a strain measurement has a magnitude of 5 millionths of a strain, what would that magnitude be if it were scaled into microstrain?

The next important thing to understand is how the strain amplitudes relate to the deformation of the FDS sensor’s bottom plate.

Example 2:

The base plate of the FDS sensor shown in Figure 2 is approximately 0.50 inches long. If the sensor is adhesively mounted to a beam and measures a strain of 9µε, how much has the length of the base plate changed? Given this measured strain is the plate in tension or compression?

Figure 2: Base Plate of the FDS Sensor Under Strain

Review of Strain and Acceleration Data

To measure the vibration response of the cantilever beam at different locations, dynamic strain and acceleration data were measured at both the free and fixed ends of the cantilever beam. This data was measured to validate the expected response of the beam. The cantilever beam was expected to have low strain and high acceleration amplitudes at the free end while having high strain and low acceleration at the fixed end. Figures 3 and 4 show measured strain time waveforms collected at the free and fixed ends of the beam, respectively.

Figure 4: Strain Time Waveform Collected at the Fixed End of the Beam

With the time waveforms plotted on common scales, it can be seen that very low strain amplitudes were measured at the free end of the beam, while the fixed end of the beam experiences much higher strain amplitudes. The vibration of the beam occurs primarily at the beam's first natural frequency and decays due to the damping of the steel. Since the tip of the beam was depressed before being released, causing the beam to vibrate, the strain amplitudes initially increased to a positive value since the top of the beam, where the strain was measured, was in tension. Acceleration data was then collected at both ends of the beam under the same condition to compare the relationship of the acceleration amplitudes at each different mounting location.

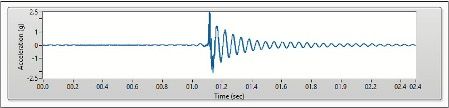
Figures 5 and 6 show the acceleration time waveforms collected at the fixed and free ends of the beam, respectively.

Figure 5: Acceleration Time Waveform Collected at the Fixed End of the Beam

Figure 6: Acceleration Time Waveform Collected at the Free End of the Beam

While strain was highest at the fixed end of the beam, the acceleration amplitudes are low at the fixed end of the beam and are higher at the free end of the beam. The acceleration amplitudes are higher at the free end of the beam because acceleration is the second derivative of displacement, and only the free end of the beam can displace.

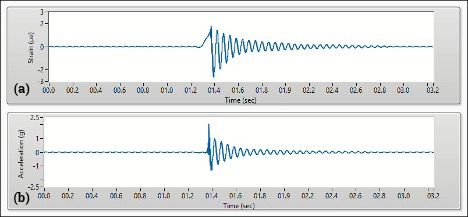
To compare the response of the beam's strain and acceleration, data was collected using a Voyager FDS sensor mounted at the fixed end of the beam and an accelerometer mounted at the free end of the beam. Figure 7 compares the time waveforms collected from both sensors in this arrangement.

Figure 7: (a) Strain Time Waveform Collected at the Fixed End, (b) Acceleration Time Waveform Collected at the Free End

Comparing these two waveforms, both the accelerometer and FDS sensor show similar vibration responses of the beam. Each time waveform shows oscillation at the beam's first natural frequency and amplitude decay due to the beam's damping. This data illustrates that both sensors can measure the response of the beam, but given the different units of measure should not be measured at the same location. It is important to remember that dynamic strain is a very different unit of measure from acceleration. Regardless of the unit of measure, the direction and location of the measurement are critical for proper data collection.

Topic of Next Video

Thank you for watching this video. The next video in this series is going to review the general operating theory of hydrodynamic bearings.